Francis HEYLIGHEN
PO, Free University of Brussels, Pleinlaan 2, B-1050 Brussels, Belgium
E-mail: fheyligh@vnet3.vub.ac.be
ABSTRACT. On the basis of the perceptual control theory of Powers, the market mechanism is analysed as a negative feedback loop which controls the deviation between demand (goal) and supply (perception) by adjusting the amount of effort invested in the production process (action), through the setting of the price. The interconnection of distributed control loops for the different products and services facilitates the allocation of production factors over the different products. The resulting global control system becomes more efficient by learning how to be more sensitive to deviations from the goal, and less dependent on the availability of resources. In that way, it resembles the nervous system of a supra-individual organism, characterized by socially distributed cognition.
Keywords: economy, perceptual control theory, control system, social system, market mechanism, learning, distributed cognition, feedback, superorganism.
When discussing social systems, it is fashionable to oppose "controlled" systems, like the plan-based economies in communist countries, to "self-organizing" systems, like the free market economies, which are governed by an "invisible hand". The net effect of the invisible hand, though, is a constraint on the economic actors, compelling them to produce specific goods for specific prices. The present paper will argue that this constraining action is functionally equivalent with control, as it is defined in cybernetics. The main difference between market control and government control will then be that the former is distributed over a multitude of interacting actors, whereas the latter is centralized in a single institution.
To analyse control in market systems, we will use the control theory of William T. Powers (1973, 1989), which was developed to model autonomous, living systems, rather than mechanical or engineering systems, which are controlled from the outside. As such, our control theoretic model will fit into the more general view of socio-economic systems as analogous to organisms. Several authors have argued that human society can be viewed as a superorganism, i.e. an organism of organisms (e.g. de Rosnay, 1975, 1996; Stock, 1993; Turchin, 1977). Powers (1992) himself, on the other hand, would restrict the use of control theory to individual organisms, arguing that social systems are essentially different. Arguments for and against the interpretation of social systems as control systems have been discussed by Heylighen and Campbell (1995). The present paper will add another argument to the case for the control interpretation.
As has been shown by Conant and Ashby (1970), the existence of control implies the presence in the controller of a model of the system being controlled. Therefore, if we can show that society is a distributed control system we will also have established the presence of distributed cognition, i.e. knowledge which is not inherent in any particular individual or institution but in the network of control loops that makes up the economy. In this most general sense, all organisms, including bacteria and plants, possess knowledge. However, in general we will only speak about cognition in higher organisms that have a central nervous system capable of learning, i.e. developing new knowledge. The final sections will suggest that the "economic organism" has such a nervous system, similar to a "global brain" (Russell, 1996; Mayer-Kress & Barczys, 1995).
Before discussing these issues, I wish to note that I am not an economist, but a cybernetician working on complex systems and cognition. As such some of the remarks I make specifically about market mechanisms may appear inaccurate or old hat to economists. Yet, I believe that a cybernetic point of view may put some well-known phenomena in a different light, and as such clarify old problems. I hope that my less-than-expert analysis of economic ideas will not detract the readers from appreciating the promises of a novel viewpoint.
In order to analyse markets as control mechanisms, we need to agree about a definition of control. Such a definition can be derived by abstraction from the example of the thermostat, which in cybernetics is viewed as the prototype of a control system. The thermostat controls the temperature in a room, keeping it within tight bounds around its reference temperature, which plays the role of a goal. This is achieved by counteracting all deviations or disturbances from that goal state, which are caused by fluctuations in outside temperature. When the temperature becomes lower than the reference temperature, the thermostat senses the change (perception) and switches on the heating (action). This increases the temperature until the reference level is reached. At this moment, the heating is switched off again. This elementary control system is also an elementary cognitive system, since in order to function it needs to "know" how to evaluate its perceptions, and how to choose the right action for each of its perceptions (Heylighen, 1990; De Mey, 1982). The two states of the thermostat, "on" and "off", in fact model the two states of the world, "temperature too low", and "temperature high enough".
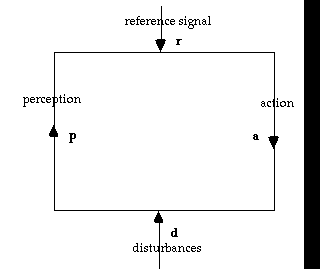
William Powers, the founder of Perceptual Control Theory (1973, 1989), has proposed the following more general scheme to represent such negative feedback control mechanisms (Fig. 1).

Fig. 1: Powers's control scheme.
The scheme consist of a feedback loop with two inputs, the reference signal r and the disturbance d. The arm of the loop going from r to d is called the action, a. The one going from d to r is called the perception, p. The relation between these elements should be such that the perception is brought as closely as possible to the reference signal, by the action compensating for the effect of the disturbance. In the simplest case, each component can be represented by a one dimensional variable, and the relation between them by two linear expressions:
a = K (r - p) (1)
p = E (d - a) (2)
The action is proportional to the difference between the reference level and the perceived level. The larger this deviation ("error") between perception and goal, the larger the correcting action needed. Similarly, the perceived state is proportional to the difference between the disturbance and the compensating action. K and E are two constants expressing characteristics of the control system. To better understand their meaning, the system of equations can be solved for a and p. This produces the following expressions:
![]() (3)
(3)
![]() (4)
(4)
Until now, the whole scheme is symmetric with respect to permutations of (r, a) with (d, p). In Fig. 1, we can turn the loop upside down, and then the reference becomes the disturbance and the action becomes the perception. However, this does not accord with our intuitive understanding of control as an asymmetric relation, in which the controller (r and a) controls the perturbations (d and p), but not the other way around. The asymmetry can be introduced by assuming that K is very large, and much larger than E. In that case, through equation (4), p becomes almost equal to r:
K >> E then p ~=r (5)
This means that control is achieved: the deviation between goal and perception is practically reduced to zero. Whatever the size of the disturbance d, the control system manages to keep the state very close to its preferred state r. K expresses the factor of "amplification": the smallest deviation (r - p) is immediately sensed and compensated by a large action a = K(r - p). Although the action is large relative to the deviation, it is in general it is not large in absolute terms (as expressed by eq. (3)). The reason is that because of the negative feedback relation the deviation is immediately compensated before it can grow larger. Thus, since deviations remain small (by equation (5)), really large actions will never be needed. The amplification factor measures both the "power" of the control system, in the sense of the amount of energy it has available to take action, and its "sensitivity", in the sense of the precision with which it reacts to the tiniest deviations.
Since the scheme is symmetric in E and K, we can make a similar interpretation of the implications of a large factor E. This would mean that the perception is very sensitive to disturbances, in other words that small perturbations would make the system deviate strongly from the reference level. This describes a situation with poor or no control. In conclusion, the larger K with respect to E, the less the perception will deviate from the goal, and the better the control.
Let us go back to the example of the thermostat. This does not perfectly fit in the above scheme, since the scheme is continuous: actions will continuously increase or decrease depending on the sensed deviations. Traditional thermostats, on the other hand, have discrete actions: either the heating is switched on or it is switched off. Let us instead assume that a corresponds to a continuously varying intensity of heating. In that case, r corresponds to the reference temperature of the thermostat, d to the heat loss caused by the lower outside temperature, and p to the actual temperature in the room. K will then basically measure the power of the heating installation: the more heat is produced per time interval, the quicker the deviation (r - p) will be corrected, and the smaller it will remain. E will then measure the sensitivity of the room to heat flow: the larger the room or the better the insulation, the smaller E, the less the outside temperature will influence the inside temperature p, and the less corrective action a the thermostat will need to take. We noted that in a traditional thermostat the state of the environment is mapped onto a discrete variable with two possible values, "on" and "off". In the continuous thermostat, or in Powers's scheme, on the other hand, the control system has a model of the world consisting of a one dimensional variable with an infinite number of possible values.
Let us try to apply this control scheme to the market mechanism. We need to find a cycle or feedback loop with two or more inputs, one of which can be identified as a goal or reference level, while the others can be interpreted as disturbances. As shown by Richardson (1991, p. 62), Adam Smith's original argument in which he proposed the "invisible hand" of the market can be represented by such a feedback cycle. I have slightly rephrased the components of this loop so that the parallelism with Powers's control scheme becomes most clear (see Fig. 2).
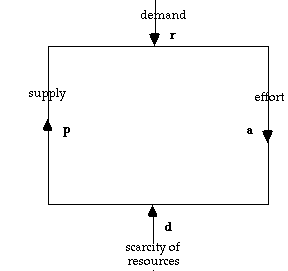
Fig. 2: the market mechanism as a control loop.
The demand for goods and services plays the role of a goal or reference level, a desire that the market tries to satisfy. We here understand demand as the amount of commodities the consumers are capable and willing to purchase, independently of whether these commodities are available or not. (Note that this is different from the way demand was understood in an earlier paper (Heylighen & Campbell, 1995), where it reflected what consumers want on top of what is already available. In the present paper this would be seen as the deviation or error signal. This different interpretation explains why the earlier paper did not treat demand as an input but as a dependent variable, and therefore did not recognize it as the goal of a control loop).
The supply is what is really available to satisfy the demand. The difference between demand and supply determines the error signal. This is reflected by the price of the commodity: the larger the discrepancy, the more expensive the good. If there is no disparity, i.e. if any demand whatsoever is completely and immediately fulfilled, the price is nil. An example of such a commodity would be air, which is everywhere plentiful. (The fact that air is normally free does not mean that people would not be willing to pay for it in a situation where it would be rare, e.g. while diving or on a space ship. Therefore, in the present usage of "demand", there is always a demand for air.) In some countries, tap water is free as well. This is an exceptional situation, however: for most commodities, there will always be moments when consumers would like to have more than is presently available. In economics, this deviation from the ideal or goal state is called "scarcity".
The larger the discrepancy between what the consumers want and what they have, the more they will be willing to pay for what they lack. This increases the incentive for producers to produce more of the scarce good. Therefore, they will invest more capital, labor and research (in short, "effort") in production. However, in order to produce goods, they depend on the availability of resources (e.g. raw materials, energy, components) over which they have no direct control. The more scarce these resources, the more difficult it will be to produce a sufficient amount of goods. Therefore, the scarcity of resources plays the role of an outside disturbance. Effort and resources together (the "factors of production") determine the total production and therefore the supply.
Although this scheme is of course highly simplified, ignoring many other factors and interactions, the negative feedback loop with two independent inputs, consumer demand and availability of resources seems well established. In order to determine whether this is really a control system, we need to investigate whether there is amplification. Let us therefore try to map the different components of the supply-demand loop onto the variables in equations (1)-(4), keeping in mind that we are working with a highly idealized model. Equation (1) then merely expresses the fact that the amount of effort invested in production will be proportional to the difference between demand and supply, as signalled by the price. Equation (2) seems at first sight counterintuitive, until we note that the signs of the different variables are purely conventional. By replacing E by -E in (2), we get a formula that tells us that the supply will be proportional to the effort invested minus the scarcity, or, in other words, to the effort plus the availability of resources.
Now we need to estimate the relative size of the two constants E and K. Let us consider an example. Imagine a poor Ethiopian farming community dependent on water for growing their crops. The amount of water they need on the land determines the demand. The amount of rain determines the availability of resources. The supply will depend on the rain and on the effort invested in irrigation, pumping, combating evaporation, etc. Obviously, in this case, whether supply meets demand will depend much more on the natural phenomenon of rain than on human effort. There is little control, and K is small with respect to E.
Now imagine a similar scenario in a rich, technologically developed region, e.g. California. The methods for irrigation and pumping are much more sophisticated, getting water from much farther away with much less loss or evaporation. In this case too, a drought will increase the price of water, but the capability of the producers to respond to the demand will be much less dependent on the natural availability. K will be much larger than E, and the system will have much better control over the amount of water needed for agriculture. The slightest increase in the need for water will immediately lead to a larger volume of water being pumped to the farms.
Let us analyse in more detail which factors determine amplification and therefore control. High K means high sensitivity to changes in the difference between supply and demand. These changes will be expressed in the fluctuations of the price. The price is determined in the market, the place where producers and consumers, buyers and sellers, meet. By coming in contact with many consumers, producers will get an idea of how much demand there really is. By looking at the proposals of competing producers they will get an idea of how much supply there really is. By comparing the average demand with the average supply they will get an idea of what price they can realistically ask for their good or service. Sensitivity means that they will immediately raise prices if demand increases, or diminish prices if supply increases, thus affecting the investment in further production.
The mechanism is not so simple or automatic as it is usually portrayed. Imagine a small market in an Ethiopian village where there are just a few buyers and a few sellers of different agricultural products. Prices will fluctuate strongly depending on the bargaining power of the consumer the producer happens to be discussing with. If suddenly a rich consumer with a high need appears, prices will jump up. Although this may seem like high sensitivity, what is sensed is in general not a reliable measure of the overall need of the Ethiopian population. There is simply too little information about the demands and supplies of the people who happen not to be present on that particular day on that particular market. The fact that a producer managed to sell his produce for a high price today, does not in the least imply that he will be as lucky the next day. Therefore, there is little incentive for him to immediately increase his production.
Now, by way of contrast, imagine the world-wide, computer controlled stock exchange. Any order to buy a particular stock, coming from any part of the world, will immediately, in whatever small amount, raise the price of that stock. Any order to sell will similarly lower the price. The effective price is a continuously adjusted average resulting from hundreds of thousands of buy/sell decisions. If we ignore the effects of speculation at this point, the price of a stock is an extremely sensitive and reliable measure of overall demand and supply. As soon as the price starts moving up, producers will start raising their production. The difference with the Ethiopian market is the immediate transmission and integration of information from all different parts of the market.
In addition to sensitivity, the amplification factor K, as we said, depends on the "power" of the control system to act. In this case, power corresponds to the amount of production factors (capital and labor) that is available to increase production. The richer the economy, the more capital will be available for investment, and the more quickly new production lines can be started up. (This again distinguishes the Ethiopian economy from the Western one.) This capital should not only exist, it should also be able to quickly move to the place where it is needed. This is usually called "liquidity" in economics.
Let us now look at the factor E, which measures the effect of disturbances on production. A good control system will be characterized by low E, i.e. low sensitivity to fluctuations in the amount of resources. This can be achieved in two ways. First, resources or products can be stockpiled. This creates a reserve, buffering against changes in availability. For example, if water is collected in a large reservoir, the distribution of rain fall over the year will have little effect on the daily distribution of water. Second, productivity can be increased. This means producing more output (goods, services) with less input (resources, labor). Buckminster Fuller (1969) noted that technological advances lead to a continuing decrease of the input needed to produce a given output. He called this evolution towards doing more with less "ephemeralization". Low buffering can be compensated by high productivity. When productivity is high, a relatively small number of goods need to be kept in store, since it is easy to produce more when demand increases. This principle underlies the trend towards "just in time" production.
In conclusion, it is clear that technological progress and increasing wealth lead to an ever tighter control over supply by the consumer's demand, making supply virtually independent of fluctuations in the availability of resources. For example, in developed economies fruits and vegetables remain available throughout the year, while the seasonal fluctuations in price tend to become smaller and smaller. Although it could be debated whether a primitive economy is really a control system, there is little room for such argument when discussing developed economies.
In our simple model, we have represented supply and demand by one-dimensional variables. In reality, there are different supply and demand variables for each of the millions of goods and services provided in society. The supply of each of these goods will be governed by a control loop. However, these loops are interdependent. One thing they have in common is the amount of effort and resources invested in the production of any one good. The total amount of effort and resources available in a society is in first approximation constant. What is used for the production of one commodity cannot be used simultaneously for the production of another commodity. The strength of the market is its capacity to efficiently allocate these "factors of production", i.e. to distribute them over the different control loops.
The principle is simple: product control loops where the deviation between supply and demand is large will be characterized by high prices and will therefore attract more factors of production. Those where the deviation is relatively small will attract only few factors of production. However, if production would decrease too much because of that, the deviation and therefore the price will go up, thus again attracting more production factors. This allocation of production factors can be seen as a higher order, collective control system, which coordinates the control loops for the individual products. Its goal is not to let any deviation become too large with respect to other deviations. Its action consists in the movement of production factors from low deviation loops to high deviation ones.
This global coordination of control loops is complemented by local interactions between control loops. For example, if the demand for cars increases, this will spur car manufacturers to assemble more cars. However, to do that they will need more components. This will increase the demand for goods such as tyres and steel. The control loop for tyres will thus be subordinated through its reference level to the control loop for cars (see Fig. 3). The control loop for steel, on the other hand, will only be partially dependent on the demand for cars, since steel is also needed for other products, like cans, buildings, bridges, etc. All control loops are thus linked via different interactions, where the reference level or resources for one control loop are partially or completely determined by the functioning of other control loops.
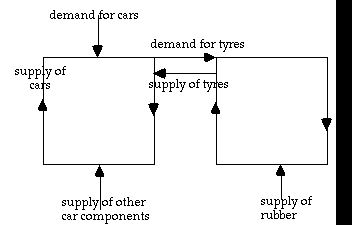
Fig. 3: example of an interaction between two control loops, where the right loop, controlling for tyres, is subordinated to the left one, controlling for cars.
Such a fluid regulation of investment and exchange is difficult to achieve in a more traditional, centralized control system. Centralized economies need to plan how much they want to invest in each of the different types of production. (Planning control is based on feedforward rather than feedback). This leads to the well-known "calculation problem": an enormous amount of information needs to be collected and processed in order to find the optimal allocation of investment over all the different production lines. In the distributed, market system, decisions to shift investment from one product to another are made locally, without knowledge of the global distribution of investment. It is the control loop which will reward (and thus reinforce) good investments, and punish (and thus inhibit) bad investments. Thus, investments are continuously flowing from one place to another while staying only in those places where there is a large enough demand with respect to the supply. This guarantees a relatively balanced distribution of labor and capital, with a minimal need for information processing.
Does the efficiency of distributed market control mean that there is no need for control by the government, as the laissez-faire economists argue (cf. Heylighen & Campbell, 1995)? Not at all. The efficiency of the market is in making sure that demand is met. However, demand is a given variable, a "reference signal" which enters the control loop from outside, but which is in general not itself under control. This would not be a problem if demand would represent the objective needs of society. In practice, however, demand represents what consumers are ready to pay for a certain good or service. This obviously depends on how much money the consumers possess. Poor consumers may have high needs, but they contribute little to the demand for the products they need. In the limit, a person with no money would effect no demand whatsoever, and would therefore be completely ignored by the control loop.
The fact that money is limited causes other paradoxical effects. In the Giffen paradox (cf. Stigler, 1947), increasing the prize of a particular good, say bread, may actually increase its sales, in contradiction with the traditional law of supply and demand. Imagine a situation where poor people divide their fixed food budget over inexpensive bread and expensive meat. A higher price for bread means that they will have less money left to buy meat. But since they need a minimum amount of calories to survive, they will compensate for less meat consumption by consuming more bread, thus increasing the demand for bread.
Wealth and poverty tend to be self-reinforcing. Poor people do not have the means to get a good education, to start a business, to invest money, or do any of the other things which typically lead to high income. This vicious circle or positive feedback loop can only be broken by outside intervention, e.g. by the government providing free education, or subsidizing business start-ups.
Positive feedback is a more general problem affecting the demand variable. A traditional example is speculation, where an increasing demand makes people anticipate even higher prices, and thus gains for goods or assets bought now and sold later. Another example is technological development, where increased adoption of an innovative technological product (say a particular type of video cassette or computer operating system) diminishes the costs needed to produce further units, and encourages the public to use that technology, rather than less well-spread competing designs. Thus, increase of supply leads to increase of demand ("increasing returns", see Arthur, 1989). On the other hand, demand for the competing design will diminish, even though that design may be objectively superior (e.g. the Betamax standard for video cassettes).
Such positive feedback loops can severely distort or destabilize the economic system. The only way not to let them get out of hand is to control the demand. This is typically done by governments through taxes or restrictions when they want to reduce demand (e.g. for alcohol, tobacco or polluting products, or during currency speculation), or through subsidies when they want to strengthen demand (e.g. for new technologies, public transport or education). Controlling the reference variable in a control loop defines a second order control system, i.e. a metasystem (Heylighen, 1995). Such a system is potentially much more flexible and intelligent than a first order system. It seems that government control is more effective when it is applied at the metalevel (the demand, i.e. the goal of the market control loop), than at the object level (the production, i.e. the means to achieve the goal). The reason is that control at the metalevel is much simpler, since all object level fluctuations in supply are already minimized by the highly effective market.
Controlling the negative effects of market mechanisms seems more effective by feedback control of its reference levels than by completely substituting it with a planning economy. This seems to be the lesson that can be drawn from the collapse of communist regimes and the success of socially adjusted market economies. The question remains open which is the most efficient way to implement such second order control of the economy. Perhaps a more distributed system may here too be worth exploring. For example, it has been proposed to control pollution by providing firms with a limited number of tokens, each entitling the owner to generate one unit of pollution, which can be bought or sold. In such a system, highly polluting factories would need to buy a lot of tokens from less polluting factories. This would make them less competitive and thus spur them to become less polluting themselves.
The picture of the socio-economic system we see emerging is that of a complex control system, consisting of an intricate network of connected control loops for the different products and services. The overall goal of the control system is to satisfy the needs of the society, both directly through the demands consumers make in the marketplace, and indirectly through the government, which tries to regulate the individual demands to better reflect long-term, collective needs. The perturbations which the system tries to minimize are the internal and external fluctuations of different resources which the system needs for its survival and growth. In this view, the socio-economic system is similar to a living organism.
Like all control systems, the socio-economic system needs specialized knowledge to control the perturbations. Indeed, every combination of values for the availability of the different resources requires a specific combination of counteractions, and the system must know which action corresponds to which perturbation (Heylighen, 1994). The mapping from the set of all possible perturbations to the set of all possible counteractions defines a model of the perturbations (Conant and Ashby, 1970), and therefore a model of the environment in which the control system tries to survive. In artificial control systems, such as thermostats and automatic pilots, the model was created by the human designer. In primitive organisms, such as plants and bacteria, this model is carried by the genes, which are the result of blind variation and natural selection.
The most sophisticated control systems, such as higher animals and people, however, are moreover able to learn, i.e. to improve their control models through experience. (Powers, 1974, 1989 calls this process "reorganization"). In animals, control is implemented by the nervous system, which connects sensors (sensitive cells in the eye, ear, skin, etc.), responsible for perception, to effectors (muscles), responsible for action. In the simplest organisms, the connection of sensor to effector is direct, like in the thermostat or a simple control loop (Turchin calls this the level of simple reflexes, 1977).
In more complex organisms, though, signals coming from different external and internal sensors need to be integrated and processed by a central nervous system in order to decide about the best combination of signals that need to be sent to the effectors (Turchin calls this the level of complex reflexes, 1977). This seems similar to a market with many different products and services, where the demands for different products are processed together in order to efficiently allocate the production factors. Such a nervous system is characterized by distributed cognition: the theory of neural networks (Rumelhart & McClelland, 1986) has shown how knowledge is spread over the pattern of connecting links, rather than localized in individual neurons or groups of neurons. For economic systems, we might say that the control knowledge is not localized in individual producers or consumers, but in the network of dependencies that connects them.
At the next level of complexity, the network processing the information will change its connections depending on its experience. The more complex and changing the environment, the greater the need to continuously adapt and fine-tune the different connection strengths. Some of the mechanisms to change connection strengths, such as back propagation and Hebbian learning, are well known through computer simulations of neural networks (Rumelhart & McClelland, 1986). We might speculate that similar mechanisms underlie the development of an economy. As a first step towards elaborating and testing this hypothesis, we may look for analogies between individual learning and socio-economic learning, which may provide inspiration for developing a more sophisticated theory.
The simplest level at which learning seems to occur is in the evolution of the control constants E and K. Like we showed in our example of the Ethiopian community compared with Western society, K tends to increase with social and technological development. Since K measures sensitivity of actions to deviations from the reference level, the process seems similar to sensitization, the process by which an organism becomes more sensitive to important stimuli. Similarly, the decrease of E, which measures the sensitivity to outside perturbations, seems analogous to habituation, the process by which an organism learns to ignore irrelevant stimuli. This analogy is quite superficial, though, since the technological development because of which E and K change is much more complicated than the mechanism underlying habituation and sensitization in neurons.
Habituation and sensitization take place on the level of the simple control loops. Learning on the level of complex networks is based on the process of association, the strengthening of connections between neural pathways. A classical learning mechanism is reinforcement, which underlies the more complex mechanism of back propagation in neural networks. Reinforcement strengthens neural connections that contribute to achieving the organism's goals, while weakening those that move it away from those goals. An analogue of such a connection in the economy would be the dependence of one control loop on the products of another loop, like in the example of the car manufacturers needing steel.
Suppose that car producers can either use steel or plastic to build their cars. This determines two connections, from plastic to cars and from steel to cars. Suppose that thanks to new technologies the producers using plastic manage to produce more cars than those using steel, for the same amount of investment and for the same quality of the final product. In that case the connection from plastic to cars will be reinforced, while the one from steel to cars will be weakened. One way to represent such learning might be to assume that the constant Ecar-plastic measuring the sensitivity of car production to plastic supply decreases, relative to the constant Ecar-steel measuring the sensitivity to steel supply. This would increase the demand for plastic coming from car manufacturers, while decreasing its demand for steel to a larger extent. The resulting overall lower sensitivity to plastic or steel supply means amplification of car production, and therefore better satisfaction of the demand for cars. This is a reinforcement of the shift in the connection strength.
A second, more indirect mechanism of association is Hebbian learning, where the connection between neural pathways is strengthened when the two pathways are activated simultaneously. For example, assume that each time the demand for cars increases the demand for petroleum also increases. There is no direct dependency of petroleum production on car production, or vice versa. Yet, the petroleum producers would be wise to watch the demand for cars, and to increase their production as soon as they see the demand for cars increase. This would allow them to anticipate the increase in demand for petroleum which is likely to follow the increase in demand for cars.
The perceptual control model seems to offer many promising insights into the functioning of economic systems. It in particular may provide a more solid, possibly even mathematical, basis for the approaches which view societies as similar to organisms. However, this will require a much more detailed analysis of the functioning of market mechanisms in terms of control loops. In particular need of study are the precise definition of the different variables of the control loop, such as supply, demand, scarcity, effort, the quantitative dependencies of these variables (as expressed in a simplified way by the constants E and K), the connections between the control loops for different products and services and the role of metalevel control by the government.
An even more challenging issue for further research is the cognitive development of the economic control system. The analogies with neural mechanisms of learning we proposed barely scratch the surface of this problem domain. Further inspiration may be found in some more detailed models for distributed, supra-individual learning via computer networks which we proposed earlier (Heylighen & Bollen, 1996; Bollen & Heylighen, 1996). Computer and communication technologies provide particularly effective ways to implement an efficient "nervous system" for the socio-economic organism. We already discussed the example of the computer-controlled stock exchange to illustrate the enormous gains in sensitivity that can be achieved in that way.
In addition to the software agents and learning hypertext webs discussed in our earlier papers, the software technology based on "workflow" holds particular promise. The main idea behind workflow is that tasks, belonging to a larger project, are automatically sent by the computer system to the person or group best qualified to handle them. Once a part of the job has been finished, the provisional results together with the subsequent questions are forwarded to the next one in line, and so on. For example, the manufacture of cars requires the completion of a number of subtasks, such as buying tyres, steel, plastic, etc. An automated computer system, when receiving an order for a certain amount of cars would automatically order the required amounts of tyres and other components to the suppliers that make the best offer, and continuously monitor in how far the orders are fulfilled. By comparing orders fulfilled by different producers, it might even learn which suppliers are most reliable and efficient and take this into account when making further orders.
Such technologies could make the socio-economic system much more efficient and intelligent, providing it with a real "global brain" (Heylighen & Bollen, 1996; Russell, 1996; de Rosnay, 1996; Mayer-Kress & Barczys, 1995). Further development of the control system model of the economy and the distributed cognition structure characterizing it may help us to support that development.
The author is supported as a Senior Research Assistant by the FWO (Fund for Scientific Research-Flanders).
Arthur W. B. (1989): "Competing Technologies, Increasing Returns, and Lock-in by Historical Events", The Economic Journal 99, pp. 106-131.
Bollen J. & Heylighen F. (1996): "Algorithms for the self-organisation of distributed, multi-user networks. Possible application to the future World Wide Web", in: Cybernetics and Systems '96 R. Trappl (ed.), (Austrian Society for Cybernetics), p. 911-916.
Buckminster Fuller R. (1969): Utopia or Oblivion (Bantam, New York).
Conant R. C. & Ashby W.R. (1970): "Every Good Regulator of a System Must Be Model of that System", Int. J. Systems Science 1:2, p. 89-97.
De Mey M. (1982): The Cognitive Paradigm (Reidel, Dordrecht)
de Rosnay J. (1975): Le Macroscope (Seuil, Paris)
de Rosnay J. (1996): L'Homme Symbiotique (Seuil, Paris),
Heylighen F. (1990): Representation and Change. A Metarepresentational Framework for the Foundations of Physical and Cognitive Science, (Communication & Cognition, Gent).
Heylighen F. (1994) "Fitness as Default: the evolutionary basis for cognitive complexity reduction", in: Cybernetics and Systems '94, R. Trappl (ed.), (World Science, Singapore), p.1595-1602.
Heylighen F. (1995): "(Meta)systems as constraints on variation", World Futures: the Journal of General Evolution 45, p. 59-85.
Heylighen F. & D. T. Campbell (1995): "Selection of Organization at the Social Level: obstacles and facilitators of Metasystem Transitions", World Futures: the journal of general evolution 45:1-4 , p. 181.
Heylighen F. & J. Bollen (1996): "The World-Wide Web as a Super-Brain: from metaphor to model" in: R. Trappl (ed.): Cybernetics and Systems '96 (Austrian Society for Cybernetic Studies), p. 917.
Mayer-Kress G. & C. Barczys (1995): "The Global Brain as an Emergent Structure from the Worldwide Computing Network", The Information Society 11 (1).
Powers W. T. (1973): Behavior: the Control of Perception, (Aldine, Chicago).
Powers W. T. (1989): Living control systems, (Control Systems Group, Gravel Switch: KY).
Powers W. T. (1992): "Control Theory Psychology and Social Organizations", in: Living Control Systems II , Powers, W. (ed.), (New View Publications, Chapel Hill, NC), p. 91-127.
Richardson G.P. (1991): Feedback thought in social science and systems theory (Univ. Pennsylvania Press, ).
Rumelhart D.E. & McClelland J.L. (eds.) (1986): Parallel Distributed Processing: Explorations in the Microstructure of Cognition, (Bradford Books/MIT Press, Cambridge, MA).
Russell P. (1996): The Global Brain Awakens: Our next evolutionary leap (Global Brain).
Stigler, G. J. (1947): "Notes on the History of the Giffen Paradox," Journal of Political Economy, 55, p. 152-156.
Stock G. (1993): Metaman: the merging of humans and machines into a global superorganism, (Simon & Schuster, New York, ).
Turchin V. (1977): The Phenomenon of Science. A cybernetic approach to human evolution, (Columbia University Press, New York).