William T. Powers, the founder of  Control Theory, has proposed the following general scheme to represent negative feedback control mechanisms. This scheme is very similar to our scheme for control except that it tries to be quantitative, whereas ours is qualitative. By the fact that it is quantitative, there are no sharp distinctions between different cases of control, but only larger or smaller values of the relevant variables. This is in particular interesting for the asymmetry of control, which is automatically assumed in our scheme, while in Powers' scheme it derives from the fact that one variable is much larger than another one.
Control Theory, has proposed the following general scheme to represent negative feedback control mechanisms. This scheme is very similar to our scheme for control except that it tries to be quantitative, whereas ours is qualitative. By the fact that it is quantitative, there are no sharp distinctions between different cases of control, but only larger or smaller values of the relevant variables. This is in particular interesting for the asymmetry of control, which is automatically assumed in our scheme, while in Powers' scheme it derives from the fact that one variable is much larger than another one.
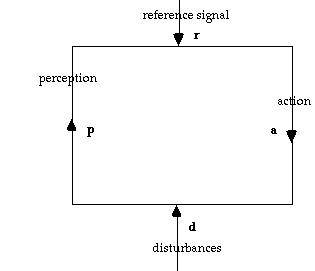
The scheme consist of a feedback loop with two inputs, the reference signal r (equivalent to our "goal") and the disturbance d. The arm of the loop going from r to d is called the action, a. The one going from d to r is called the perception, p. The relation between these elements should be such that the perception is brought as closely as possible to the reference, by the action compensating for the effect of the disturbance. In the simplest case, each component can be represented as a one dimensional variable, and the relation between them by two linear expressions:
| a = K (r - p) | (1) |
| p = E (d - a) | (2) |
The action is a function of the difference between the reference level and the perceived level. The larger the deviation between perception and goal ("error"), the larger the correcting action needed. Similarly, the perceived state is a function of the difference between the disturbance and the compensating action. K and E are two constants expressing characteristics of the control system. To better understand their meaning, the system of equations can be solved for a and p. This produces the following expressions:
| a = KE(r/E - d)/(KE + 1) | (3) |
| p = KE(r - d/K)/(KE - 1) | (4) |
Until now, the whole scheme is symmetric with respect to permutations of (r, a) with (d, p). In Fig 1, we can turn the loop upside down, and then the reference becomes the disturbance and the action becomes the perception. However, this does not accord with our intuitive understanding of control as an asymmetric relation, in which the controller (r and a) controls the perturbations (d and p), but not the other way around. The asymmetry can be introduced by assuming that K is very large, and much larger than E. In that case, through equation (4), p becomes almost equal to r:
K >> E => p ~= r
This means that control is achieved: the deviation between goal and perception is practically reduced to zero. Whatever the size of the disturbance d, the control system manages to keep the state very close to its preferred state r. K expresses the factor of "amplification": the smallest deviation (r - p) is immediately sensed and compensated by a large action a = K (r - p). Although the action is large relative to the deviation, as expressed by eq. (3), it does not need to be large in absolute terms. The reason is that because of the negative feedback relation the deviation is immediately compensated before it can grow larger. Thus, really large actions will never be needed, since deviations always remain small. The amplification factor measures both the "power" of the control system, in the sense of the amount of energy it has available to take action, and its "sensitivity", in the sense of the precision with which is responds to the tiniest deviations.
Since the scheme is symmetric in E and K, we can make a similar interpretation of the implications of a large factor E. This would mean that the perception is very sensitive to disturbances, in other words that the tiniest perturbation would make the system deviate from the reference level. This describes a situation with poor or no control. In conclusion, the larger K with respect to E, the less the perception will deviate from the goal, and the better the control.
See also:

