PESP, Free University of Brussels, Pleinlaan 2, B-1050 Brussels, Belgium
ABSTRACT. It is argued that the analysis and control of complex systems demands a completely new, non-classical framework, based on a distinction dynamics. Dynamical representations are analysed as distinction systems. Classical representations are characterized by the fact that all distinctions are conserved. The creation, conservation and destruction of distinctions can be understood on the basis of a distinction dynamics. The fundamental mechanism is the variation through recombination and selective retention of closed combinations. The fact that the same process may be constrained by several independent closures is emphasized. Complex dynamics is analysed as an example of a theory with a limited dynamics of distinctions: distinctions can be destroyed but not created. It is sketched how a more general theory might be applied in solving complex problems in the form of a computer program based on variation and selection.
Table of Contents:
The analysis and control of complex and dynamic systems clearly demands a methodology and conceptual framework which is different from that used in classical science, where the typical objects under study (e.g. atoms, planets moving around the sun, simple mechanical systems) behave in a way which is regular and predictable. Complex systems, on the other hand typically behave in ways which are difficult to predict, and where both chaos, and new order, may emerge. The present paper aims to give a short overview of a new conceptual framework which has been developed since several years. This approach attempts to go beyond the limitations which are inherent in the classical way of modelling. Therefore one of the first steps in its development had to be an analysis of the implicit assumptions of classical science, which is exemplified by classical physics.
This analysis starts with the dynamical representations of systems, which are the mathematical models allowing to make predictions about the evolution and control of the system. The components of a representation are shown to be reducible to "distinctions", which are primitive elements of structuration. In classical representations all distinctions are invariant. Complex, non-mechanical systems on the other hand are characterized by self-organization, and hence by the spontaneous emergence of new distinctions. In order to describe such systems in the most general way, we need a dynamics of distinctions. The basic principles of such a distinction dynamics will be outlined. As an example of a non-classical theory where there is a non-trivial dynamics of distinctions, the theory of complex dynamics will be discussed.
The domain of application of this approach consists in the first place in the computer modelling of complex systems and problem domains. Therefore it is sketched how the basic principles of a distinction dynamics can be implemented on a computer, and how the resulting program could support people involved in the managing of complex, self-organizing systems.
Mathematical models are ways to represent dynamical systems in the most precise way possible, in order to allow prediction of the future states of the system, given knowledge about the present state. Such a model of a process will be called a dynamical representation. A representation should here not be understood in the sense of a homomorphic image of an objective, external reality, but as a system designed to give a more or less precise, mathematical shape or structure to the associations between different observations (this is similar to the sense of "representation" as it is used in mathematics, or in the phrase "knowledge representation", cf. Heylighen, 1990b). For example, it is possible to construct a representation of a "black box" system just by establishing mathematical relations between the inputs to which the system is submitted and the outputs which are observed. This representation may be adequate in predicting the behaviour of the system, without therefore implying any correspondence between the formal components of the representation and the (hidden) material components of the system.
Let us analyse the standard components of a dynamical representation. First there are the objects representing the system to be modelled or its components. Objects might stand for electrons, molecules, planets, etc. Objects are characterized by variable properties or predicates, such as position, mass, charge, velocity, ... The attribution of a particular predicate to a particular object, e.g. electron e has position P, determines an elementary proposition describing the system. Propositions can be combined by means of logical connectives (conjunction, negation, disjunction ...) in order to form compound propositions. A proposition which gives all the information one can get about the system at a particular instant in time is called the state of the system. The set of all possible states is called the state space. The evolution of the system can then be described by a time-parametrized trajectory in the state space, representing the states of the system at subsequent instants. In order to determine the trajectory, one needs two further structures: operators and dynamical constraints. An operator is a transformation or transition rule mapping initial states onto subsequent states. A dynamical constraint is a selection criterion which determines which of the possible state transitions corresponding to different operators will actually take place. Dynamical constraints usually have the form of either 1) differential (or difference) equations, relating the predicted state transition (time derivative of the state) to the present state, 2) conservation principles, stating that a certain global property of the system, e.g. energy, must be conserved during the transition, or 3) variation or optimization principles, stating that that transition will occur which minimizes (or maximizes) a certain function of the transition parameters.
These different components of a dynamical representation correspond to ways of structuring the domain of experience (i.e. the possible observations and their relations) in such a way that the resulting system is as simple, precise, and reliable as possible. Since a representation is necessarily less complex than what it is to represent (the whole actual and potential domain of experience), this means that a number of observed features must be abstracted out, by putting different phenomena, which are similar with respect to the problem one tries to solve, into the same class, and by distinguishing this class from other classes of phenomena. The distinctions can be conceived as elementary structurations of a domain of experience (Spencer Brown, 1969), hence as elements or units of representation. A representation as a whole can then be analysed as a network of distinctions connected by certain relations, i.e as a distinction system (Heylighen, 1988).
The components of a representation correspond to particular types of distinctions. An object corresponds to a distinction between the focus of attention (figure, pattern, system) and its background or environment. A predicate corresponds to the distinction between the class of all objects with a certain property and the complement of that class. A proposition corresponds to the distinction between the truth of a certain description and its falseness (or truth of the negation of the proposition). Time corresponds to a distinction between past, present (i.e. simultaneity) and future. An operator corresponds to a distinction between the state before the operator was applied and the state afterwards. A dynamical constraint corresponds to a distinction between an allowed state transition, and an impossible one.
Classical representations, exemplified by the theory of classical mechanics, are based on the paradigm that all change can somehow be reduced to the movement in space of separate, rigid objects, following trajectories completely determined by physical laws. The typical illustration is the movement of planets around the sun, or of billiard balls on a table. The space in which the system is moving is in general an abstract configuration or phase space. The classical evolution of a system is causal, deterministic and reversible, and its representation is supposed to be objective, i.e. independent of the observer.
Let us look at the behaviour of the different types of component distinctions of a classical representation. Objects are supposed to have an invariant identity: during their movement they do not disappear or merge with other objects, and no objects are created out of the void, or by the breaking up of existing objects. In other words, the distinction between object and background is always conserved. An object is supposed either to have a certain property, or not to have it. The attribution of a predicate to an object is objective, and all observers are supposed to agree upon it. Hence the distinction between having a property and not having it is also invariant. The same applies to propositions which are either true or false, independently of the observer, and to the time-ordering of two events, which are either simultaneous, or the one precedes the other one. Hence propositional and temporal distinctions are also invariant. Again the same principle applies to dynamical constraints: a transition is either allowed or not allowed, without any ambiguity. Finally the principle applies to state trajectories: two trajectories starting at distinct states at a certain instant will always remain distinct, and have always been distinct. This is the principle of absolute causality, encompassing reversibility and predictability (Heylighen, 1989b).
In conclusion, all distinctions between objects, between predicates, between different trajectories, between truth and falsity, between past and future, and between possible and impossible, are invariant: they remain the same for all times and for all observers. This absolute distinction conservation can be taken to be the defining characteristic of the classical way of representation.
The only thing which can vary is the actual combination of predicates which determines the state, but this variation is completely constrained by the trajectory which is determined by the dynamical constraints. The trajectory is closed in the sense that the system must follow a given trajectory: it cannot leave it and follow another trajectory, or it cannot enter from another trajectory, since the reversibility and predictability of classical evolution precludes any branching of trajectories. Mathematically, the trajectory may be called linearly closed (i.e. there is a complete, linear order relation between the points on the trajectory).
Let us first formulate some general principles about the way distinctions change or maintain. The cinematics of distinctions can be viewed as a general description of possible processes involving distinctions. For a given type of distinction there are four types of processes (cf. Heylighen, 1989b):
| number | 1. | 2. | 3. | 4. |
| type | conservation of all distinctions | destruction of distinctions, without creation of new ones | creation of new distinctions, and maintenance of the existing ones | creation and destruction of distinctions |
| relation | one-to-one, | many-to-one, | one-to-many | many-to-many |
| bijective | surjective | |||
| process | ||||
| past | reversible | irreversible | reversible | irreversible |
| future | <predictable | predictable | unpredictable | unpredictable |
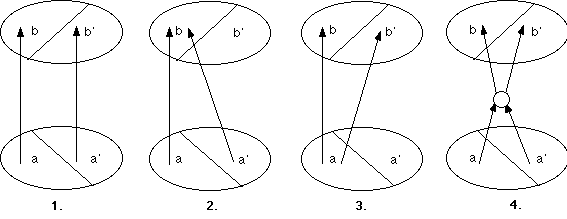
These 4 types of processes can be easily represented by denoting a single distinction by the couple (a, a') of a class a and its complement a' (Heylighen, 1989b; 1990b). Conservation of the distinction means that the couple is sent bijectively onto another couple (b, b'): a -> b, a' -> b'. The other types of processes are depicted in fig. 1.
By considering different types of distinctions, a much more complex classification of distinction processes can be made. For example, a process can conserve type A, destroy type B, and create-and-destroy type C, hence it could be characterized by the combination A.1, B.2, C.4. Moreover, the class of the process may vary according to the time interval, so that a particular type of distinction is conserved during interval [ t1, t2 ], but destroyed during the subsequent interval [ t2, t3 ].

Figure 1: four basic types of distinction processes: 1. conservation, 2. destruction, 3. creation and 4. creation-and-destruction.
After classifying possible distinction processes (cinematics), we must understand the constraints which will select the actually occurring processes out of the potential ones (dynamics). In order to do that we will assume that general processes belong to class 4., and that it is possible to conceptually separate the phases of creation and of destruction of distinctions. The creation phase may be called "variation", since it creates a variety of distinct configurations or "variants". Variety (Ashby, 1964) can here be understood as a measure of the amount of distinct configurations. The second phase may be called "selection" since it reduces variety by selectively eliminating certain variants, thus destroying distinctions.
The basic dynamical principle governing this process states that those variants will be eliminated which are unstable (i.e. which tend to spontaneously disappear because of their own internal dynamics, or because they are not adapted to their environment). The stable ones, on the other hand, will be selected and hence "survive". This principle is just a simplified, tautological version of the Darwinian principle of natural selection. "Tautological" does not mean "trivial", however. The value of a tautology resides in its use as rule for "rewriting" and thus simplifying a description, in the same sense as the laws of logic (e.g. the laws of de Morgan, or the principle of contradiction) are tautologies, but yet are very useful when making complex inferences.
In order to allow such non-trivial inferences we must analyse in more detail what are the mechanisms of variation and the criteria of selection ("stability"). The selection we want to understand is not so much the selection of a separate variant, but of the distinction between the variant and its environment. In other words, we are looking for a criterion for the invariance of distinctions. This invariance can be defined mathematically by means of the concept of (relational) closure (Heylighen, 1989a, 1990a).
In mathematics closure can be defined as an operation C on sets, C: B -> B*, with the following properties: monotonicity, idempotence and inclusion preservation (Heylighen, 1990b). A set B is called closed if B* = B. Intuitively such a closure of a set means that somehow "missing elements" are added to it, until no more of them are needed. For example, in topology, if you want to "close" an open set, you must add the boundary to the set itself. However, the general definition does not tell us what would be missing, or when we should stop adding elements. Intuitively, a subsystem B of a global system S of elements and relations (or-more generally-connections) is closed if B can be externally distinguished from its complement (S\B) in an invariant way, whereas the internal distinctions between the elements or subsystems of B are not (or less) invariant. Examples of closure are the transitive or cyclical closure of a relation, or the closure of a group of transformations under its composition operation (Heylighen, 1989a;1990a).
Closure can be understood as an internal stability criterion, leading to selection, for a particular variant D of a subsystem distinguished from its environment, but it can also provide a criterion for the adaptation or "fit" of the variant D to one or more other systems E, F, G, ..., external to D, so that {D, E, F, G, ...,} would together form a higher-order closed system D'. In that case it is not so much D which is stabilized, but the relation between D and E, F, ..., and hence the compound system D'. It may well be that D itself loses its invariance within the larger system D'. For example, in a unicellular organism, the cell forms an (organizationally) closed unit, which is stabilized by homeostatic mechanisms. However, in a multicellular organism, it is the whole of all cells which forms a closed entity which is to be maintained, and this stability of the whole is relatively independent of the continuous destruction (through aging or natural processes) of many of the cells which constitute its parts.
Variation in this framework can be modelled by considering change as the result of changed relations between invariant elements (closed subsystems or "modules"), in other words as the recombination of modules. For example, sexual reproduction which is one of the basic variation mechanisms in biological evolution consists of the recombination of chromosomes from two organisms. This is an example of external variation, whereby the modules to be recombined with the original modules come from outside the original closed system (organism), and hence are in a certain respect "new" or "unpredictable".
In a dynamical representation, on the other hand, variation is modelled by a transition between states, whereby a state is determined by a specific combination of elementary propositions, consisting of objects and predicates, e.g. "the particle has position x" & "the particle has momentum p". A new state will consist of a different combination of objects and predicates. This is an example of internal variation since all the possible predicates and objects are already contained within the representation system as a whole. This may be called the closure of the state space: no (internal) variation process can generate a state which does not belong to the state space: though the state changes, the state space itself is invariant.
Internal variation is thus constrained by the closure of the system to which it belongs. The stronger the closure, the more constrained the variation, and the more predictions can be made about the process. However, it must be noticed that purely random variation (in the sense that all possible outcomes have an equal probability) is also closed, since probability can only be defined as a measure on a (closed) set of possibilities. A dynamical evolution is internal (or closed) whenever there exists a fixed state space (or set of possible outcomes) in which the process takes place.
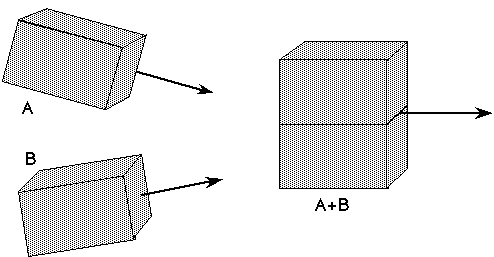
Figure 2: two magnets A and B, together determining a 12-dimensional configuration space, stick together forming the compound object A+B, which moves in a 6-dimensional configuration space
External variation on the other hand, can be understood as a process in which the constraints, and hence the state space (and the representation), change during the evolution. For example, a rigid body (e.g. a glass), moving according to the laws of classical mechanics, may break, creating two rigid bodies, again moving according to the laws of classical mechanics, but now in a state space with the double number of degrees of freedom. Similarly, two separate rigid bodies (e.g. magnets) might undergo a mutual attraction and stick together, forming one aggregate rigid body, thus reducing the dimension of the state space by a factor 2 (see fig. 2). None of these processes (which occur all the time in real life) can be represented in a classical framework, where there is no dynamics of distinctions.
External variation can also be understood as the result of internal variation and external selection. A process can follow a trajectory which is completely determined by a closure constraint internal to the system. However, suddenly the process may reach a state which is not only closed according to this constraint, but also according to another constraint, external to the original system. An illustration would be example of the magnets, where one magnet may follow a determined trajectory until it suddenly comes into contact with the other magnet. Now another stronger constraint appears, which makes it impossible for the first magnet to continue its trajectory, since it sticks to the second magnet. The state with the two magnets sticking together is clearly selected out of the possible two-magnet states, since it is more stable than a state with the two magnets moving around in each other's neighbourhood. The selection corresponds to a new closed distinction, namely the one where the two magnets together are distinguished as one object, instead of as two separate objects. The selection is however external to the original closed dynamics of the first magnet's movement.
Another example is problem-solving. During problem-solving potential solutions are sequentially generated following a certain algorithm or heuristic. This heuristic rule expresses an internal constraint. However, even if the rule would completely determine all the states which can be tried out, this rule alone is not sufficient to determine where the solution can be found. Discovering the solution of a problem is typically an "Aha!" experience, which is sudden and unexpected: everything "falls into place" (forms a closed "Gestalt", see Stadler & Kruse, 1990) when one of the states generated by the heuristic appears to fulfill the selection criterion which defines the problem. If the closure defining the solution would be the same as the closure which constrains the search process, then problem-solving would be trivial, because everything would be constrained beforehand, and it would suffice to apply a given function to the initial state in order to get the solution or final state. What is specific about problem-solving is that there are two a priori independent selection criteria: an internal one (heuristic), which constrains variation, and an external one (defining the goal), which determines the end of the variation when the problem is solved. What characterizes a good heuristic is that the way it constrains generated combinations of representation elements resembles as much as possible the constraint determining the solution.
This paradigm for distinction dynamics is still relatively simple since there are only two closure constraints. In general, however, multiple selection criteria, constraining variation in multiple systems, and selecting stable states composed of multiple single system states, will be functioning. A somewhat more complicated example is biological evolution. There are basically two types of variation processes here: 1) mutation, which is random but internal to the genome of an organism, considered as an (organizationally) closed system; 2) recombination of chromosomes in sexual reproduction, which is external to the single organism but internal to the species considered as a closed system for the operation of mating; this variation is not completely random since it is constrained by criteria such as sexual attractiveness. Besides these variation processes there are many external selection criteria determined by the environment (adaptation), by the internal stability of the organism (spontaneous abortions can be considered as variations eliminated by internal stability criteria), by the reproductive capacity of the organism ("fitness" is defined as the expected number of offspring).
Processes like this may be called "self-organizing", since there is no global (internal or external) constraint which controls or "organizes" the process. In a mechanical system, on the other hand, there is a complete closure, controlling the variation in a deterministic way, so that predictions can be made about future states. In a self-organizing system there are different interacting constraints, some of which only become apparent aftere a certain state is reached, resulting in the emergence of a wholly new state space, with new distinctions. We will now discuss one particular type of approach, which has recently become popular, and which is capable of representing certain of these processes.
Probably the most fundamental concept in complex dynamics is that of an attractor. An attractor is a region of state space such that the trajectory of a dynamical system can enter the attractor but cannot leave it (and such that the region has no subattractors). The existence of attractors is clearly in contradiction with the classical principle of reversibility: if evolution were reversible, then for each trajectory leading into the attractor there would be an inverse trajectory leading out of the attractor. In traditional thermodynamics the attractor consists of just one point, the equilibrium or maximum entropy state. In non-linear, far-from-equilibrium models, however, an attractor can have a much more complex structure. The simplest non-point attractor is a one-dimensional limit cycle (see Fig. 3), but it is also possible to have attractors with multiple dimensions (e.g. a torus for 2 dimensions), or even fractal dimensions (so-called strange or chaotic attractors).
The entering of an attractor can be seen as a phase of distinction destruction. This is obvious for point attractors or limit cycles, since distinct initial states (in the attractor basin) lead to the same final state, which is periodically (cycle) or continuously (point) repeated. In multidimensional or strange attractors the situation is more complicated, however, since they contain in general an infinity of trajectories (within a finite volume), so that it is difficult to observe whether two initially distinct trajectories would merge inside the attractor.

Figure 3: a 1 -dimensional attractor or limit cycle.
The arrows correspond to trajectories starting outside the attractor, but ending up in a continuing cycle along the attractor.
A better way to study the dynamics of distinctions here is to replace individual, discrete distinctions by a continuous measure of the amount of distinctions. Such a measure, determining the amount of distinct states, may be called variety. The simplest example of a variety measure would be the volume of the state space region (dependent on the metric of state space). In classical mechanics, there is the Liouville theorem stating that the volume of state space is conserved during dynamical evolution, and this is just another way of expressing that all distinctions are conserved in classical mechanics. In complex dynamics, on the other hand, state space volumes are clearly not conserved, since the volume of the attractor basin (all states whose trajectories will end up inside the attractor) is generally larger than that of the attractor itself (that part of the basin which contains no subattractors). If the volume of the attractor is zero, however, this way of measuring distinction destruction is rather indiscriminate, since it does not distinguish between different shapes or dimensions of attractors. The (fractal) dimension of the attractor would be a better measure in this case. In general it would seem that there are several ways of measuring the variety of an attractor, but no universal one.
The entering of an attractor can be interpreted as a reduction of the state space of the system: once it is in the attractor all the states outside the attractor become unreachable, the only states the system could still attain are those inside the attractor. The example of the two magnets (Fig. 2) can be analysed in this framework. Each magnet, as a rigid body, has 6 degrees of freedom for moving in three-dimensional space. The compound system constituted by both magnets hence has 12 = 6 x 2 degrees of freedom. However, the situation where the two magnets are stuck together, forming one rigid body instead of two, can be viewed as an attractor for the state space with 6 degrees of freedom. Hence the reaching of the attractor has reduced the dimension of state space from 12 to 6.
An attractor can be seen as a part of the state space closed under the dynamics of the system. This closure, however, is different from the closure constraining the trajectory, and the reaching of the attractor (selection of the "closed" set of states) cannot be predicted from the knowledge of the dynamical law. This is nicely illustrated by the "computational irreducibility" of cellular automata. A cellular automaton is a very simple, computational model of a complex, but deterministic dynamic system. It has been shown by Wolfram (1984) that it is generally impossible in principle to predict whether a given initial state of the automaton will or will not end up in an attractor of the dynamics, because a potentially infinite number of state transitions has to be computed in order to rule out that a given state would be repeated after a certain number of periods, thus determining a one dimensional attractor (limit cycle). The closure corresponding to the attractor belongs to a different, "emergent" order with respect to the closure of the dynamical process which constrains the state transitions.
The attractor concept clarifies how distinction destruction occurs in complex dynamics. The creation of distinctions is more subtle, however. By definition, the dynamical systems studied in complex dynamics are deterministic or predictable, which means that no distinctions between state trajectories are created: equal causes (initial states) have equal effects (further trajectories) (Heylighen, 1989). However, if we look at the system from a more global or macroscopic viewpoint (i.e. not tracking all microscopic transitions along an individual trajectory), we may find some phenomena which very much look like distinction creation.
For example, if a parameter describing the dynamical configuration is varied, we may find that for a certain value of that parameter the number of equilibrium states or point attractors suddenly increases. This is called a bifurcation (Prigogine, 1979): the attractor splits in two (or more). The newly emerging region in between the two separated attractors is unstable. This means that a point in that region will fall either into the one or into the other of the attractors, depending on which of the two attractor basins it belongs to. However, the boundary separating the two basins will in general be very difficult to discriminate exactly (it may for example have a fractal shape), so that it is practically impossible to determine to which of the two basins the point belongs, and hence in which of the two attractors it will end up. This is called sensitive dependence on initial conditions: two initial states may be arbitrarily close together, yet they may end up in attractors which are arbitrarily far apart. If the parameter is further varied we may find that the number of bifurcations increases exponentially until a regime is reached where an infinity of attractors is dispersed all over state space, in such a way that an attractor can be found arbitrarily close to any point of state space. Such a regime is completely chaotic: the final equilibrium state of the system could be anywhere in state space, depending on the slightest differences in initial conditions.
It is such sensitive dependence on initial conditions, meaning that states which are initially arbitrarily close together may end up arbitrarily far apart, which leads to an apparent distinction creation on a macroscopic level. The arbitrarily small distance between initial conditions means in practice that the initial conditions cannot be distinguished by a necessarily limited measuring device; the arbitrarily large distance between "final" conditions, on the other hand, is evidently distinguishable by normal means. Hence, it appears as if a distinction between two macroscopical configurations "emerges out of nothing".
The "stretching" of pieces of state space in complex dynamics is not a real creation of distinctions, however. Though it is possible to describe a reduction of the state space as the entering of an attractor, the opposite phenomenon: the expansion of state space (and its dimension), cannot be represented in complex dynamics. The simplest way to conceptualize such an expansion would be to increase the number of components or objects in the representation (for example when an object breaks in two), but we could also conceive of an increase in the number of predicates. Moreover, complex dynamics can only describe one state space reduction, based on a single closure. In order to describe more general processes in a precise way, a completely new theory, based on the distinction dynamics will have to be constructed. We will not go into detail of how such a theory would look mathematically, but instead sketch how such a theory might be applied to practical problem situations.
The concepts and principles introduced above should not remain purely theoretical speculations. With the advent of the new information technology complex, qualitative mechanisms can now be implemented and tested on computer in a relatively simple way. A general programming paradigm, pattern directed systems, is emerging, which is directly applicable to the present type of approach. A pattern directed system consist of a collection of modules or rules, which respond to messages ("conditions") characterized by a specific pattern (i.e. a set of variables or input channels structured in a specific way) by sending out new messages ("actions"), dependent on the information received. The system is intrinsically parallel since different modules can respond simultaneously to the same (or different) message(s), but it is possible to simulate such mechanisms on sequential machines. Examples of pattern directed systems are : production systems, classifier systems, object-oriented systems, and logical or relational programming.
In our approach the modules can be likened to (sub)systems, the messages to their input and output. Two modules can be said to be (temporarily) coupled if the output message of the one is accepted as input by the other one. The general problem with pattern directed systems is to specify the control structure, i.e. the set of rules which determines which module can send or accept messages to or from which other module. The generalized variation-selection dynamics in combination with the closure concept may provide an answer to this problem.
The dynamics controlling the flow of messages must depend on two types of selection criteria: the external "problem", to be specified by the user, and the internal closure of collections of coupled rules, leading to the self-organization and emergence of complex subsystems within the pattern directed system. In order to be effective the system must also have a variation mechanism. In order to start the problem-solving (= evolution) process, there must be an original variety of modules. This can be provided by the user, who could try to express the initial knowledge he has about the problem domain in the form of "if ... then ..." modules. Of course, this initial variety can allways be expanded by the user during the problem-solving process: there is a continuous interaction between the computer system and the user, who plays the role of the external environment. Another source of variety can be provided by the computer system itself, which generates variations of the existing modules by internal changes or by combinations with different, external modules. Until now, typical problem-solving programs (working according to the generate-and-test mechanism) only use internal variation, i.e. the state of the system is changed by replacing some of its intrinsic properties. However, we have shown that external variation is a more interesting process in the sense that it can give rise to the emergence of higher-order systems through closure.
An example of an existing pattern directed system evolving through variation-selection is formed by "classifier systems" (Wilson, 1987). Here the selection is basically external, but the variation is partially internal ("mutation" of classifiers), partially of a mixed type ("recombination" of classifiers, in which part of one module (=classifier) is recombined with part of another module). There is no explicit closure mechanism. Moreover, the information contained in a module is fixed, so that there is no explicit mechanism for emergence, although complex "assemblies" of modules might implicitly develop.
Let us conclude by sketching how a pattern directed implementation of the present theory of emergence and evolution might be applied to "real world" problems. The main idea would be to design a generic computer support system for solving complex problems (Heylighen, 1989b; 1990c). A problem, can be defined as a situation of non-optimal or non-satisfactory adaptation. The problem does not need to be well-structured (i.e. have an explicit goal, initial state and domain), it suffices that the actor experiencing the problem be capable of distinguishing satisfactory solutions from non-satisfactory ones, i.e. that he be able to carry out a selection between possibilities offered to him. The task of the support-system would then be to provide the user with potential solutions, with a relatively high probability of success. Therefore the system must possess some intelligence, i.e. use the available (though usually incomplete) knowledge in an efficient way by integrating the pieces of knowledge in stable, adaptive systems or complexes, and adapt itself rapidly to new input from the user. Moreover, the proposed potential (or partial) solutions should be meaningful to the user, i.e. easily recognizable as satisfactory or not.
Therefore, the organization of the proposed system should be transparent and intuitive. This demands an advanced interface for representing complex information. Such an interface may be provided with the aid of so-called "hypermedia" (Heylighen, 1990c), i.e. the combination of multiple media (text, graphics, sound, programming, animation...) in a non-sequential, but easily accessible, network format. The network consisting of chunks (representing concepts or subsystems, separated by distinctions) and links (representing connections between subsystems) can be easily edited by the user, and analysed by the system in search of closure. The interaction between user and system makes it possible to restructure the representation in order to find the simplest or most adequate model for searching solutions or evaluating solutions to the complex problem which is posed (Heylighen, 1990c).
HEYLIGHEN F. (1988) : "Formulating the Problem of Problem-Formulation", in: Cybernetics and Systems '88, Trappl R. (ed.), (Kluwer Academic Publishers, Dordrecht), p. 949-957.
HEYLIGHEN F. (1989a): "Coping with Complexity: concepts and principles for a support system", in: Preceedings of the Int. Conference "Support, Society and Culture: Mutual Uses of Cybernetics and Science", Glanville R. & de Zeeuw G. (eds.), (IWA, University of Amsterdam), p. 26-41.
HEYLIGHEN F. (1989b): "Causality as Distinction Conservation: a theory of predictability, reversibility and time order", Cybernetics and Systems 20, p. 361-384.
HEYLIGHEN F. (1990a) : "Relational Closure: a mathematical concept for distinction-making and complexity analysis", in: Cybernetics and Systems '90 , R. Trappl (ed.), (World Science Publishers, Singapore).
HEYLIGHEN F. (1990b): Representation and Change. A Metarepresentational Framework for the Foundations of Physical and Cognitive Science, (Communication & Cognition, Gent).
HEYLIGHEN F. (1990c): "Design of an Interactive Hypermedia Interface Translating between Associative and Formal Problem Representations", to be published in International Journal of Man-Machine Studies.
PRIGOGINE I. (1979): From Being to Becoming : Time and Complexity in the Natural Sciences, (Freeman, San Francisco).
SPENCER BROWN G. (1969): Laws of Form, (Allen & Unwin, London).
STADLER M. & KRUSE P. (1990): "Theory of Gestalt and Self-organization", in: Self-Steering and Cognition in Complex Systems, Heylighen, Rosseel & Demeyere (eds.), (Gordon and Breach, New York), p. 142-169.
WILSON S.W. (1987): "Classifier Systems and the Animat Problem", Machine Learning 2, p. 199-228.
WOLFRAM S. (1984): "Computation Theory of Cellular Automata", Comm. Math. Physics.96, p. 15.