The model of evolution, discussed in Quasispecies, implies a strong assumption:
the selective value is determined by the Hamming distance between the
particular and unique master sequences. Only one maximum of the
selective value exists. Using the physical spin-glass concept, we
can construct a similar model for a very large number of the local
maxima of a selective value.
D. Sherrington and S. Kirkpatrick proposed a
simple spin-glass model to interpret the physical properties of
the systems, consisting of randomly interacting spins [1]. This
well-known model can be described shortly as follows:
| ; |
1) There is a system S of
spins Si , i =
1,..., N (the number of spins N is
supposed to be large, N >> 1). Spins take
the values: Si = 1,
-1 . |
| ; |
2) The exchange interactions between spins are
random. The energy of the spin system is defined as: |
| |
E (S)
= - Si<j Jij
Si Sj ,
|
(1) |
| |
where Jij are the
exchange interactions matrix elements. Jij
are normally distributed random values: |
| |
Probability_density{Jij
} = (2p)-1/2
(N-1)1/2 exp [- Jij2
(N-1)2-1] . |
(2) |
From (1), (2) one can obtain, that the mean
spin-glass energy is zero (<E > = 0) ,
and the mean square root value of the energy variation at
one-spin reversal is equal to 2:
| MSQR {dE
(Si -->
- Si) } = 2 . |
(3) |
The model (1), (2) was intensively investigated.
For further consideration the following spin-glass features are
essential :
- the number of local energy minima M is
very large: M ~ exp(aN)
, a = 0,2 ;
(a local energy minimum is defined as a state SL
, at which any one-spin reversal increases the energy E );
- the global energy minimum E0
equals approximately: E0 = - 0,8 N .
Let's construct the spin-glass model of evolution
[2]. We suppose, that an informational sequence (a genome of a
model "organism") can be represented by a spin-glass
system vector S . The evolved
population is a set {Sk}
of n sequences, k = 1,..., n. The
selective values of model "organisms" Sk
are defined as:
| f(Sk)
= exp[- b E(Sk)]
, |
(4) |
where b is the selection
intensity parameter.
The definition (4) implies that the model genome Sk
consists of different elements Ski ,
which pairwise interact in accordance with the random interaction
matrix Jij . In order to maximize
the "organism" selective value (that is to minimize the
energy E(S)), it is necessary
to find a such combination of elements Si
, that provides maximally cooperative interactions for given
matrix Jij .
As in Quasispecies , we suppose,
that 1) the evolution process consists of consequent generations,
2) new generations are obtained by selection (in accordance with
selective values (4)) and mutations (sign reversals of sequence
symbols, Ski --> - Ski
, with the probability P for any symbol) of sequences Sk
. The initial population is supposed to be random.
The described spin-glass model of evolution was analyzed by
means of computer simulations and rough estimations [2]. The main
evolution features are illustrated by Fig.1. Here n(E)
is the number of sequences S , such
that E(S) = E in a
considered population; t is the generation number.
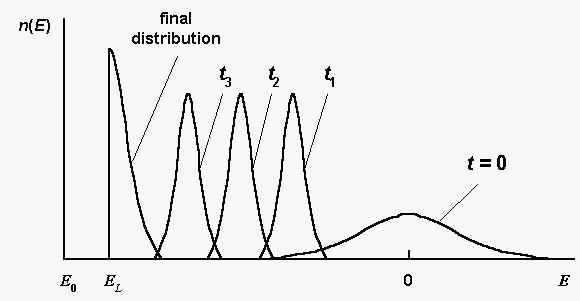
Fig. 1. The sequence distribution n(E)
at different generations t ; t3 >
t2 > t1 ; E0
and EL are global and local energy
minima, respectively; the global energy minimum E0
equals approximately: E0 = - 0,8 N.
Schematically, according to the computer simulations [2].
The spin-glass-type evolution is analogous to the Hamming
distance case (see Quasispecies, Estimation of the evolution rate). But
unlike the Hamming-distance model, the evolution converges to one
of the local energy minima EL ,
which can be different for different evolution realizations.
Because one mutation gives the energy change dE ~ 2 (see (3)), and the
typical time for one mutation per sequence dt
is of the order (PN)-1, the total number
of evolution generations T (at sufficiently large
selection intensity b) can be
estimated by the value T ~ (|E0|/dE)xdt
~ (0.8N /2)x(PN)-1. This value
is close to the estimation of value T in the
Hamming-distance case. So, the estimations of the evolution rate
are roughly the same for both models, and we can use formulas
(1)-(3) in Quasispecies to characterize
the spin-glass-type evolution as well.
Analogously to the Hamming-distance case, we can consider the
sequential method of energy minimization, that is the consequent
changes of symbols (Si --> - Si)
of one sequence and fixation only successful reversals. The
sequential search needs smaller participant number than the
evolution search. Nevertheless, the evolution search provides in
average a more deep local energy minimum EL
[2], because different valleys in energy landscape are looked
through in evolution process simultaneously with descending to
energy minima.
Thus, in the spin-glass case, the evolutionary search has a certain
advantage with respect to the sequential search: it provides in
average the greater selective value.
Conclusion. The spin-glass model of evolution
refers to the "organisms", which have many randomly
interacting genome elements. Evolution can be considered as a
search of such genome elements, which are able to cooperate in
the most successful manner.
References:
1. D.Sherrington , S.Kirkpatrick. //
Physical Review Letters. 1975. V.35. N.26. P.1792. S.Kirkpatrick,
D.Sherrington. // Physical Review B. 1978. V.17. N.11.
P.4384.
2.V.G.Red'ko. Biofizika. 1990. Vol. 35.
N.5. P. 831 (In Russian).

