M. Eigen and P. Schuster proposed the model of
hypercycles [1], as a hypothetical stage of macromolecular
evolution, which could follow quasispecies.
The hypercycle is a
self-reproducing macromolecular system, in which RNAs and enzymes
cooperate in the following manner (Fig.1): there are RNA
matrices ( Ii ); i-th
RNA codes i-th enzyme Ei (i
= 1,2,...,n); the enzymes cyclically increase RNA's
replication rates, namely, E1 increases
replication rate of I2 , E2
increases replication rate of I3 , ..., En
increases replication rate of I1 . In
addition, the mentioned macromolecules cooperate to provide
primitive translation abilities, so the information, coded in
RNA-sequences, is translated into enzymes, analogously to the
usual translation processes in biological objects. The cyclic
organization of the hypercycle ensures its structure stability.
For effective competition, the different hypercycles should be
placed in separate compartments.
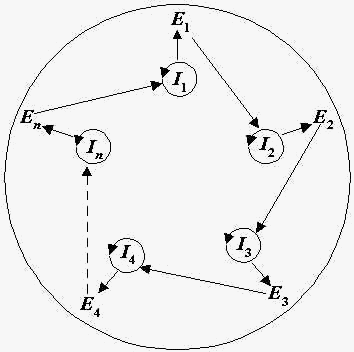
Fig. 1. Hypercycle structure. Ii
are RNA matrices, Ei are replication
enzymes (i = 1,2,...,n).
The replication enzymes ensure the more accurate
RNAs' replication as compared with quasispecies, providing
opportunities for further macromolecular structure improvements.
M. Eigen and P. Schuster consider hypercycles as predecessors of
protocells (primitive unicellular biological organisms) [1].
Let's review shortly the mathematical description
of hypercycles, taking into account the original model [1] as
well as the analysis by R.Feistel, Yu. M. Romanovskii, and
V.A.Vasil'ev [2], who modeled a hypercycles competition in
coacervate-type compartments.
We suppose, that 1) the hypercycles are placed
into coacervates [3]; 2) each coacervate includes only one type
of the hypercycles; 3) any coacervate volume is proportional to
the number of macromolecules inside it; 4) a translation process
is much quicker than a replication one (the latter means that it
is sufficient to consider the RNAs dynamics only [1]). Using
these assumptions, we obtain the following equations:
| dNi /dt
= Vfi , |
V = c-1 Si Ni
, |
xi = Ni
/V , |
i = 1,2,..., n, |
(1) |
where Ni and xi
are a number of molecules of i-th RNA and its
concentration in a coacervate, respectively; V is a
coacervate volume; c is a constant, characterizing a
total concentration of macromolecules in a given coacervate; fi
is a synthesis rate of i-th RNA. Values fi
are defined as:
| fi = a xi
xj , |
i = 1,2,..., n, |
j = i -1 + ndi1, |
(2) |
where a is a synthesis rate parameter
(for the sake of simplicity we assume the value a to be
the same for all RNAs in a given hypercycle), dij is the
Kronecker symbol (dij
= 1, if j = i; dij
= 0, otherwise). Eq. (2) takes into account the cyclic structure
of hypercycles (see Fig.1). From (1) we obtain:
| dxi /dt
= fi - xi
c-1 Sj
fj , |
(3) |
| dV/dt = V c-1 Sj
fj . |
(4) |
According to (2),(3), the concentration dynamics
in a particular hypercycle is described by the nonlinear ordinary
differential equations, which were analyzed [1] by qualitative
methods. The analysis showed, that if the number of
hypercycle member n is less than or equal to 4, the
macromolecules concentrations xi
converge to the following equilibrium values:
and if n > 4 the concentrations xi
converge to a stable limit cycle, that is a periodic orbit in the
concentration hyperspace. For the limit cycles, the mean values
of the macromolecules concentrations xi
are determined by the same formula [1] :
If several hypercycles have different replication
abilities, their volumes increase with different rates. Averaging
on periodic concentration oscillations (if needed), we can
deduce, that according to (4), the hypercycle, having the
greatest value
(k is the hypercycle
type index), possesses the greatest selective ability.
In order to consider the hypercycles competition
explicitly, let's suppose, that any coacervate splits into two
parts, when its volume exceeds a certain critical value, and that
the total volume of all types of hypercycles is restricted by
some constant: Sk
Vk =
VT = const (Vk is the total volume of k-th type of
hypercycles). Then instead of Eq. (4), we have:
| dVk/dt
= Wk Vk
- Vk [VT-1SkWkVk] . |
(7) |
The selective values Wk
can be calculated from (2), (3), (5), (6) [2]:
Eq. (7) is well known [1]; according to its
solution, only the hypercycle, having the
maximal selective value Wm =
maxk {Wk},
survives during competition.
Conclusion. Developing the hypercycle model,
M. Eigen and P. Schuster discussed a very profound and difficult
problem: how could the real very complex translation mechanism
and unique genetic code be created during macromolecular
self-organizing process? The problem was not solved, but
plausible evolution steps were outlined and a corresponding
well-defined mathematical model was developed.
References:
1. Eigen M. and P. Schuster.  The Hypercycle: A principle of natural self-organization, Springer, Berlin, 1979
The Hypercycle: A principle of natural self-organization, Springer, Berlin, 1979
2. R.Feistel, Yu. M. Romanovskii, and
V.A.Vasil'ev. Biofizika. 1980. Vol. 25. N.5. P. 882. (In
Russian).
3. A.I.Oparin. "The origin of
life". New York, 1938. A.I.Oparin. "Genesis
and evolutionary development of life". New York,
1968.

