We describe here the model of an adaptive syser [1], which can
modify its behavior in accordance with external environmental
change. We consider also the mini-syser and compare selective
abilities of both sysers.
The mini-syser (Fig. 1a) is a very simple syser, it includes only
such macromolecules, which are necessary and sufficient for
self-reproduction, namely, the matrix I , the
replication enzyme E1 , and the
translation enzyme E2 .
The adaptive syser (Fig. 1b) includes two additional enzymes:
the regulatory enzyme E3 and the adapting
enzyme (adapter) E4 . The regulatory enzyme E3
recognizes the environment state and "turns on" or
"turns off" the synthesis of the adapter in accordance
with the environment changes.
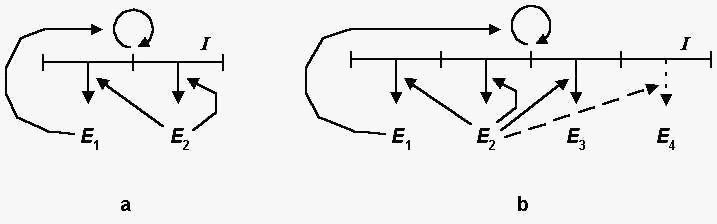
Fig 1. The schemes of mini-syser (a) and
adaptive syser (b). I is the polynucleotide matrix, E1
, E2 , E3 , and E4
are replication, translation, regulatory, and adapting enzymes,
respectively.
We suppose that there are two types of external
environment, A and B. The environment A is
a usual one, in which both sysers are able to reproduce
themselves. The environment B is unusual, in which the
macromolecular synthesis takes place only in the adaptive syser.
The regulatory enzyme E3 in the adaptive
syser is synthesized with a small rate in both A and B
environments, it recognizes the environment state and
"turns on" the synthesis of the adapter E4
in the environment B and "turns off" this
synthesis in the environment A. The adapter E4
provides the macromolecular synthesis in the adaptive syser in
the environment B.
For example, we may imply that the environment A
corresponds to the usual syser's "food", usual powerful
chemical substrate SA , and the
environment B corresponds to the usually
"uneatable" chemical substrate SB
, which can be transformed into "eatable food" SA
by means of the adapter E4. "For the
sake of economy", it is natural to synthesize the adapter
only then, when it is really needed, i.e. only in the environment
B. To recognize the environment state, the regulatory enzyme
E3, which is synthesized always, but
"economically" (with a small rate), is included in the
syser structure. The scheme of this molecular control is similar
to the classical model by F. Jacob and J. Monod [2].
To describe quantitatively the syser's features, we use the
following assumptions: 1) the different sysers are placed into separate coacervates; 2) any coacervate volume is
proportional to the number of macromolecules inside it. From
these assumptions we obtain the following equations:
| dNi /dt
= Vfi , |
V= c-1Si Ni
, |
xi = Ni
/V , |
(1) |
where Ni and
xi are the number of molecules and
the concentration of i-th macromolecules in a given
coacervate, respectively; V is coacervate volume; fi
is the synthesis rate i-th macromolecules; c is
the constant total concentration of macromolecules in a
coacervate (c = Si xi
= const); here the index i = 0 refers to matrix I,
and other i (= 1,2,3,4) refer i-th enzymes (E1
, E2 , E3 ,
E4), respectively. We define the synthesis
rates as follows.
For the mini-syser we set:
| f0 = a0
x0 x1 , |
fi = ai
x0 x2
, |
i = 1,2, |
in environment A , |
(2a) |
| f0 = f1=
f2 = 0 , |
; |
; |
in environment B . |
(2b) |
For the adaptive syser we set:
| f0 = a0
x0 x1 , |
fi = ai
x0 x2 , |
i = 1,2,3, |
in environment A , |
(3a) |
| f0 = b0
x0 x1 , |
fi = bi
x0 x2
, |
i = 1,2,3,4, |
in environment B . |
(3b) |
Here ai and bi
are synthesis rate parameters. Eqs. (2), (3) state
that the matrix/enzyme synthesis rate is proportional to the matrix
and replication/translation enzyme concentrations.
From (1) we obtain:
| dxi /dt
= fi - xi
c-1 Sj
fj , |
(4) |
| dV/dt = V c-1 Sj
fj . |
(5) |
According to (2) - (4), the concentration
dynamics in a particular syser is described by nonlinear ordinary
differential equations, which were analyzed [1] by usual
qualitative methods. The analysis showed that the macromolecules
concentrations xi converge to the
equilibrium stable state x0 = {x0i
}. In the environment A the values x0i
are expressed as (for both sysers):
| x00 =
c a0 a1 D
, |
x0i
= c ai a2 D
, |
D = [a0a1
+ a2 (a1+
... + an)]-1, |
i = 1, ..., n, |
(6) |
where n is a number of enzymes in a considered
syser (here we set a4 = 0) . For the adaptive
syser in the environment B, the equilibrium
concentrations x0i are
also determined by Eq. (6) after substitution bi
instead ai .
According to equation (5), the coacervate volume
rates are proportional to selective values:
Analogously to hypercycles,
we can consider the competition of mini-syser and adaptive syser
explicitly, supposing that the total coacervates volume for both
types of sysers should be constant. During competition, a syser, having the maximal selective value W
, is selected. Assuming small convergence time to the equilibrium
state x0 and substituting values
x0i , determined by formulas
(6), into (7) , we obtain the selective values of the considered
sysers. For the mini-syser we have
| WMini_A
= c a0 a1 a2
[a0a1 +
a2 (a1+
a2 )]-1 , |
WMini_B
= 0, |
(8) |
in the environments A and B,
respectively. For the adaptive syser the corresponding
selective values are expressed as follows:
| WAdaptive_A
= c a0 a1 a2
[a0 a1+
a2 (a1+ a2
+ a3)]-1 , WAdaptive_B
= c b0 b1
b2 [b0
b1 + b2 (b1+
b2 + b3 + b4)]-1
.
|
(9) |
These expressions show, that in the environment A
, the mini-syser has a selective advantage with respect to
the adaptive one, because WMini_A is
always greater, than WAdaptive_A .
Such a disadvantage of the adaptive syser is due to the necessity
to synthesize always the additional regulatory enzyme E3
. The disadvantage is small, if regulatory enzyme synthesis rate
is small (a3 << a1,
a2). Obviously, the adaptive syser is preferable
in the environment B.
If the environment states (A and B)
are intermittent, we can introduce the effective selective values
of the considered sysers:
| WMini = (1 - PB)
WMini_A , |
(10) |
| WAdaptive = (1 -
PB) WAdaptive_A
+ PB WAdaptive_B
, |
(11) |
where PB is the
probability of the environment B . The adaptive syser
has a selective advantage with respect to the mini-syser, if WAdaptive
> WMini . From expressions (8)-(11) we can see
that the adaptive syser is significantly preferable, if the
regulatory enzyme synthesis rate is small (a3
<< a1, a2) and the
macromolecular synthesis rate in the environment B as
well as the probability of this environment are sufficiently
large (bi ~ ai
and PB ~ 1).
Thus, the adaptive syser does have a selective
advantage with respect to the mini-syser, however not always, but
only if the "expenses", needed to support the molecular
control system operation, are sufficiently small.
Conclusion. The control system
of the adaptive syser could be the first control system, which
was "invented" by biological evolution. The adaptive
syser model demonstrates quantitatively, that the new
evolutionary invention has selective advantages, if
"invention profits" are greater than "invention
expenses".
References:
1. V.G.Red'ko. Biofizika. 1990. Vol. 35.
N.6. P. 1007 (In Russian).
2. F.Jacob and J.Monod. J. Mol. Biol.
1961. Vol. 3. P. 318.

